Une approche pour réaliser le recuit de Potts à l'aide de diodes à avalanche à photon unique
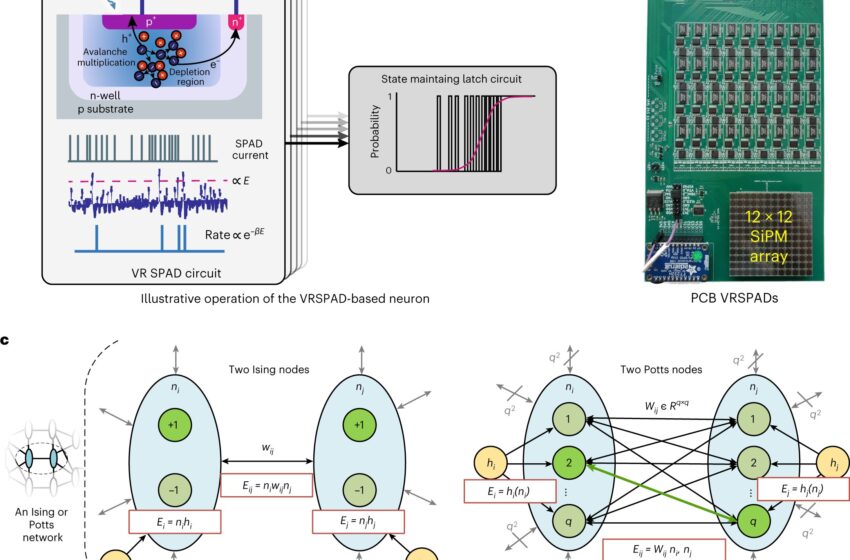
Présentation du recuit d'Ising et Potts compatible CMOS à l'aide de SPAD. Crédit: Électronique naturelle (2023). DOI : 10.1038/s41928-023-01065-0
Les processeurs de recuit massivement parallèles, dans lesquels les nœuds de calcul d'un seul processeur peuvent effectuer simultanément une série d'opérations coordonnées, pourraient présenter un énorme potentiel pour résoudre des problèmes complexes d'échantillonnage et d'optimisation. Les ingénieurs électroniciens et les physiciens du monde entier ont donc tenté de concevoir de nouvelles approches permettant la réalisation de ces dispositifs.
Des chercheurs de l'Université de Californie à Santa Barbara ont récemment introduit une méthode permettant de contrôler en continu la température de calcul et de mettre en œuvre le modèle dit de Potts, en réalisant le recuit d'Ising et de Potts à l'aide de petits dispositifs de détection de lumière connus sous le nom de diodes à avalanche à photon unique (SPAD). . L'approche proposée, décrite dans un Électronique naturelle papier, pourrait éclairer le développement futur de processeurs de recuit massivement parallèles.
“Il y a quelques années, j'assistais à une conférence du professeur Kerem Y. Camsari (co-auteur de cet article), où il parlait de son élégant travail sur l'informatique avec des bits probabilistes (p-bits) utilisant Ising (ou plus généralement des machines Boltzmann), a déclaré le professeur Luke Theogarajan, auteur principal de l'article, à Tech Xplore.
“Un composant clé du p-bit est un nanodispositif, dans ses travaux la jonction tunnel magnétique (MTJ), qui fournit la source de hasard nécessaire au calcul probabiliste. Je travaillais à cette époque sur des imageurs utilisant des SPAD et je savais que ces des appareils pourraient être utilisés pour créer des générateurs de nombres aléatoires. Cela a finalement déclenché l’idée de ce travail.
Notamment, contrairement aux jonctions tunnel magnétiques (MTJ) et à divers autres dispositifs, les SPAD peuvent être facilement intégrés à des circuits à base de semi-conducteurs à oxyde métallique complémentaire (CMOS) largement utilisés et aux processus existants de fabrication de composants électroniques. Les propriétés favorables de ces dispositifs sont ce qui a finalement encouragé Theogajaran, en collaboration avec William Whitehead, un étudiant diplômé qu'il supervise, à essayer d'exploiter ces dispositifs comme source d'entropie pour des applications informatiques dites probabilistes.
“Contrairement à d'autres approches qui utilisent les SPAD comme source de synchronisation pour un générateur pseudo-aléatoire numérique conventionnel, mon brillant étudiant diplômé William a réalisé que la physique sous-jacente conduisant à des changements exponentiels dans les fréquences d'impulsions pouvait être exploitée pour réaliser la fonction de transfert nécessaire à l'échantillonnage du Distribution Boltzmann (une caractéristique clé du calcul p-bit)”, a déclaré Theogarajan. “L'un de nos objectifs était de prouver que nous pouvions atteindre un calcul p proche de l'idéal à l'aide des SPAD. En outre, nous explorions certaines idées sur le repliement des protéines à l'aide de couplages évolutifs, qui utilisent le modèle de Potts.”
Le modèle de Potts est un cadre basé sur la mécanique statistique, qui constitue essentiellement une généralisation plus puissante du modèle d'Ising à deux états. Les professeurs Theogarajan, Whitehead, Camsari et l'étudiant diplômé Zachary Nelson du groupe de Theograjan ont conçu une approche permettant d'implémenter facilement un modèle Potts dans le matériel, ce qui n'avait jamais été tenté auparavant.
“L'un des principaux avantages de l'utilisation des SPAD est la possibilité de les intégrer facilement dans le matériel CMOS, et nous disposons actuellement de quelques prototypes simples que nous caractérisons”, a expliqué Theogarajan. “De plus, contrairement à d'autres appareils essayant d'exploiter le bruit naturel, le signal SPAD ” est une impulsion amplifiée en raison du processus de multiplication des avalanches. Peut-être que le plus grand avantage résulte de l'exploitation des exponentielles naturelles présentes dans notre matériel basé sur SPAD pour les modèles d'Ising et Potts. “
Les modèles d’Ising et de Potts font tous deux partie d’une classe plus large de cadres connus sous le nom de modèles basés sur l’énergie. Les modèles basés sur l'énergie ont été largement mis en œuvre par des chercheurs du monde entier et ont contribué à résoudre un large éventail de problèmes pratiques en refondant la fonction de coût en termes d'énergie.
“La solution la plus probable (ou probable) est la solution optimale.” » dit Théogarajan. “L'équation de l'énergie s'appelle l'hamiltonien et la probabilité d'être dans un état particulier est proportionnelle à l'exponentielle (négative) de l'énergie, ce qui est un résultat bien connu de la mécanique statistique, aboutissant à la distribution de Boltzmann. En termes simples, la distribution de Boltzmann est l'état le plus probable du système en équilibre.
Dériver la distribution dite de Boltzmann est un problème informatique difficile. En revanche, les implémentations matérielles ou expérimentales du modèle d'Ising et Potts permettent de produire des exemples d'états à partir de la distribution, plutôt que de calculer la distribution complète.
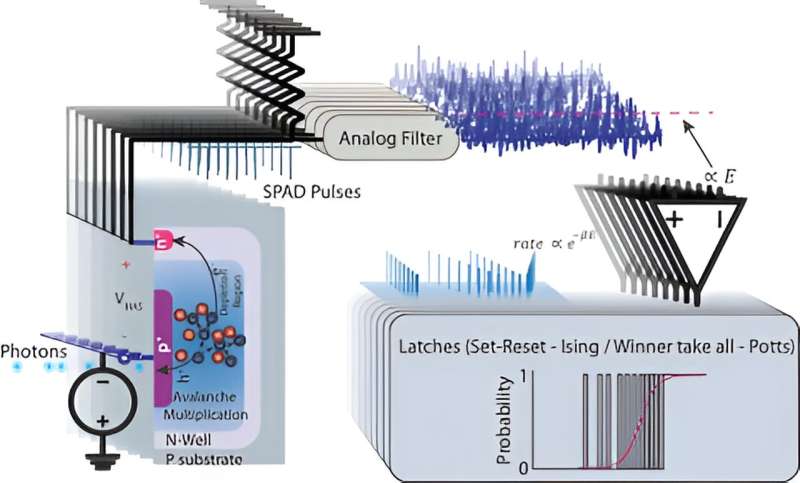
Neurones probabilistes globaux basés sur SPAD. Les photons entrants sont convertis en brèves impulsions (ou événements). Le temps entre les événements (ou taux) est converti en signal analogique via un filtre puis comparé à une tension proportionnelle à l'énergie. Plus d'événements entraînent plus de valeurs de signal dépassant le seuil d'énergie, ce qui entraîne le maintien du verrou d'état dans le même état (forte probabilité). Ainsi, le neurone produit (en moyenne) une probabilité proportionnelle à l’énergie entre les états satisfaisant l’exigence de la distribution de Boltzmann. Crédit : Figure modifiée à partir de Whitehead et al, Électronique naturelle (2023). DOI : 10.1038/s41928-023-01065-0
“Une façon de visualiser cela serait d'imaginer un paysage accidenté dans l'espace énergétique avec des collines et des vallées, chaque vallée étant un état stable”, a déclaré Theogarajan. “Le système se déplace ensuite d'une vallée (état) à l'autre avec une certaine probabilité en fonction de la différence d'énergie entre les états. Le but des tâches d'optimisation, par exemple, est de trouver la vallée la plus basse de l'ensemble du paysage énergétique (l'état). avec l'énergie la plus basse ou le minimum global) lorsque la fonction de coût est refondue en fonction énergétique. Cependant, le système peut souvent rester bloqué dans des vallées sous-optimales (également appelées minima locaux) si la barrière autour de la vallée est élevée.
Une approche proposée pour résoudre ce problème consiste à démarrer un système avec une température de calcul élevée. Cela permet au système de rebondir hors des minima locaux, en abaissant lentement la température pour identifier la solution optimale. Cette stratégie est connue sous le nom de recuit, car elle imite le processus de recuit décrit par la théorie physique.
“Alors, comment les SPAD s'intègrent-ils ici ? La fréquence d'impulsion des SPAD est intimement liée à l'heure d'arrivée des photons (ou aux statistiques des photons)”, a expliqué Theogarajan. “Il est bien connu que les statistiques des photons suivent un processus de Poisson, le temps d'arrivée entre photons est distribué de manière exponentielle. Si ce temps entre impulsions (ou taux) est converti en tension à l'aide d'un filtre et comparé à une tension représentant l'énergie, le taux résultant des impulsions de cette comparaison suivront une exponentielle proportionnelle à l'énergie, précisément ce qui est nécessaire pour mettre en œuvre la distribution de Boltzmann.
Une fois ce processus terminé, il ne reste plus qu'à convertir les brèves impulsions produites par les SPAD dans les états requis par les implémentations d'Ising et Potts. Theogarajan et ses collègues y sont parvenus en utilisant une simple technique de bascule set-reset et un mécanisme de verrouillage gagnant-gagnant pour implémenter le vecteur codé à chaud du modèle de Potts.
“Le mécanisme de verrouillage du gagnant prend tout définit essentiellement la sortie actuelle sur 1 s'il reçoit un événement et réinitialise (ou inhibe) tous les autres nœuds du vecteur formant le nœud de Potts”, a déclaré Theogarajan. “La nature événementielle de la sortie SPAD, associée au mécanisme permettant de réaliser l'exponentielle, réduit tous les calculs en un seul dispositif compact, ce qui prendrait normalement des milliers de transistors pour être réalisé. Plus important encore, la mise en œuvre de l'exponentielle est très précise car elle est liée aux propriétés physiques intrinsèques de l'appareil.
Une autre caractéristique intéressante des SPAD est qu’ils peuvent réaliser un recuit en temps réel en utilisant l’intensité lumineuse et/ou l’excès de tension de polarisation. Ce sont des variables qui peuvent contrôler la fréquence d'impulsion globale des appareils et donc également leur température de calcul.
“C'est très différent des approches de recuit actuelles, dans lesquelles les poids sont mis à l'échelle à chaque étape de recuit pour modifier la température de calcul”, a déclaré Theogarajan. “Dans l'ensemble, notre étude met en évidence la puissance du modèle Potts. En utilisant le même matériel sous-jacent, nous avons pu montrer que le modèle Potts, avec son implémentation intrinsèque à un vecteur chaud, permet d'obtenir des solutions presque 10 fois plus rapidement que l'implémentation Ising. Au meilleur de nos connaissances , il s'agit de la première implémentation matérielle directe de Potts.
Les travaux récents de cette équipe de chercheurs pourraient avoir diverses implications pratiques. Par exemple, leur approche visant à réaliser le recuit de Potts dans les systèmes matériels pourrait éclairer le développement d’outils capables de trouver des solutions approximatives aux problèmes de temps polynomial non déterministes.
“L'attribution des canaux 5G MIMO est un domaine pratique qui a des conséquences”, a déclaré Theogarajan. “Un autre exemple serait la planification d'étage pour la conception de puces. Le modèle d'Ising et Potts échantillonnant véritablement la distribution sous-jacente à l'aide de quelques exemples de formation peut également être utile dans les applications IA/ML.”
Dans leurs prochaines études, Theogarajan et ses collègues prévoient de réaliser leur implémentation du recuit de Potts sur une puce CMOS. L’équipe a déjà fait quelques progrès vers cet objectif, par exemple en vérifiant des circuits intégrés à neurones uniques en CMOS d’une taille de 65 nm.
“Ces circuits sont incroyablement petits et utilisent environ 50 µm2en comparaison un seul 231-1 générateur de nombres pseudo-aléatoires (à l'exclusion de tous les autres circuits nécessaires à la mise en œuvre de l'hyperbolique tangente) occupe environ 200 µm2 dans le même nœud technologique”, a ajouté Theogarajan. “Nous concevrons très prochainement une puce intégrant de nombreux spins/neurones ainsi que la synapse (se multiplier et s'accumuler). Nous évaluons également des architectures tirant parti du modèle de Potts pour le calcul. »
Plus d'information:
William Whitehead et al, Recuit d'Ising et Potts compatible CMOS à l'aide de diodes à avalanche à photon unique, Électronique naturelle (2023). DOI : 10.1038/s41928-023-01065-0
© 2023 Réseau Science X
Citation: Une approche pour réaliser le recuit de Potts à l'aide de diodes à avalanche à photon unique (13 décembre 2023) récupéré le 13 décembre 2023 sur
Ce document est soumis au droit d'auteur. En dehors de toute utilisation équitable à des fins d'étude ou de recherche privée, aucune partie ne peut être reproduite sans autorisation écrite. Le contenu est fourni seulement pour information.
