Extension du principe d'incertitude en utilisant un opérateur illimité
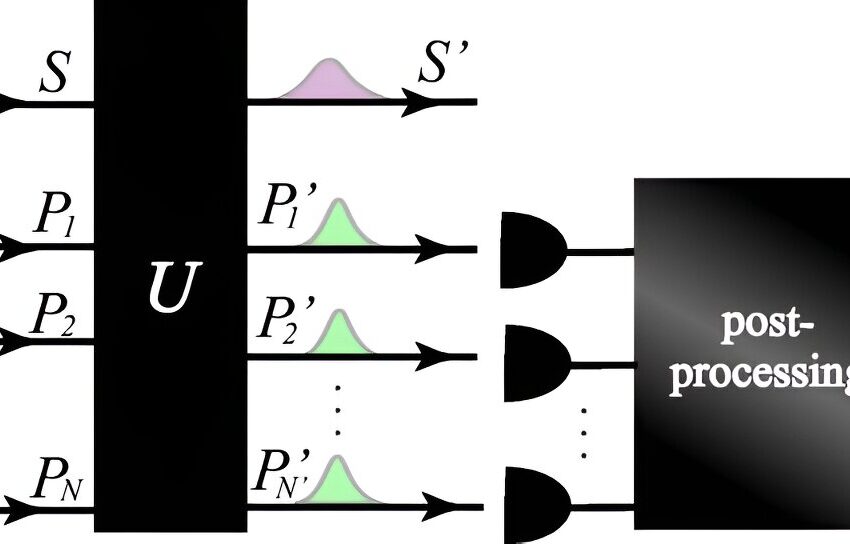
Modèle de mesure avec opérations optiques passives et mesures de comptage de photons. Crédit: Lettres d'examen physique (2023). DOI : 10.1103/PhysRevLett.131.210201
Une étude publiée dans la revue Lettres d'examen physique par des chercheurs japonais résout un problème de longue date en physique quantique en redéfinissant le principe d'incertitude.
Le principe d'incertitude de Werner Heisenberg est une caractéristique clé et surprenante de la mécanique quantique, et il peut en être dû à son rhume des foins. Misérable à Berlin au cours de l'été 1925, le jeune physicien allemand passe des vacances sur l'île isolée et rocheuse de Helgoland, dans la mer du Nord, au large des côtes nord de l'Allemagne. Ses allergies se sont améliorées et il a pu poursuivre son travail en essayant de comprendre les subtilités du modèle atomique de Bohr, en développant des tableaux de propriétés atomiques internes, telles que l'énergie, la position et l'impulsion.
À son retour à Göttingen, son conseiller, Max Born, a reconnu que ces tableaux pouvaient chacun être formés en une matrice, essentiellement un tableau de valeurs bidimensionnel. Avec Pasqual Jordan, 22 ans, ils ont affiné leurs travaux sur la mécanique matricielle – la première théorie réussie de la mécanique quantique – les lois physiques qui décrivent les petits objets comme les atomes et les électrons.
Bien que la mécanique matricielle soit remplacée d'ici quelques années par la fonction d'onde et son équation de Schrödinger, elle a permis à Heisenberg de formuler le principe d'incertitude : il existe une limite à la précision avec laquelle l'emplacement et l'impulsion d'un système quantique, généralement une particule, peuvent être déterminés. mesuré.
La limite du produit des incertitudes de mesure des deux grandeurs est h/4π, où h est la constante de Planck, extrêmement petite mais néanmoins non nulle. En bref, on ne peut pas mesurer à la fois la position et l’impulsion d’un objet quantique avec une précision arbitraire : mesurer l’un avec une précision plus élevée signifie que l’autre ne peut être mesuré qu’avec une précision moindre.
D'un point de vue physique, supposons que nous voulions mesurer la position et l'impulsion d'un électron. Il faut éclairer d’une manière ou d’une autre un système afin de mesurer ses propriétés. La lumière est quantifiée sous forme de photons, qui ont une énergie non nulle. Faire briller un photon sur l’électron perturbe nécessairement l’électron de son état d’origine. En mécanique quantique, le simple fait de mesurer impose une limite à la précision de la mesure.
Des incertitudes similaires s'appliquent aux mesures du temps et de l'énergie, de la position angulaire et du moment cinétique, et en général à deux variables qui ne « font pas la navette » lorsqu'elles sont représentées comme des opérateurs dans une mécanique quantique rigoureuse.
Quelques décennies plus tard, le principe d'incertitude a été affiné par les physiciens Eugene Wigner, puis Huzihiro Araki et Mutsuo M. Yanase dans le théorème de Wigner-Araki-Yanase (WAY), qui stipule que pour deux quantités observables q et p, où p est conservé ( comme l'impulsion d'un système), alors même si p n'est pas mesuré du tout, q ne peut pas être mesuré avec une précision arbitraire.
“Grâce au théorème WAY, nous pouvons voir que (dans un certain sens) il est impossible de mesurer la position q de la particule ; tout ce que nous pouvons mesurer, c'est sa position par rapport à l'appareil, q—Q”, a déclaré le mathématicien John Baez de l'Université de New York. L'Université de Californie à Riverside a écrit, où Q est la position de l'appareil de mesure.
Mais le théorème WAY ne s'applique qu'à des quantités comme le spin d'une particule, qui ne peut prendre que des quantités discrètes et bornées.
Yui Kuramochi de l'Université de Kyushu et Hiroyasu Tajima de l'Université des communications électroniques du Japon ont résolu un problème de longue date en montrant que le théorème WAY s'applique également aux quantités observables qui sont continues (non discrètes) ou illimitées, comme la position.
“Selon le principe d'incertitude, la position et l'élan ne peuvent pas être mesurés simultanément avec précision”, a déclaré Kuramochi. “Notre résultat donne une restriction supplémentaire : même seule la position elle-même ne peut pas être mesurée avec précision, tant que nous utilisons des mesures naturelles satisfaisant la conservation de la quantité de mouvement.” Leur preuve examine un « opérateur illimité », des quantités physiques qui peuvent prendre des valeurs infiniment grandes.
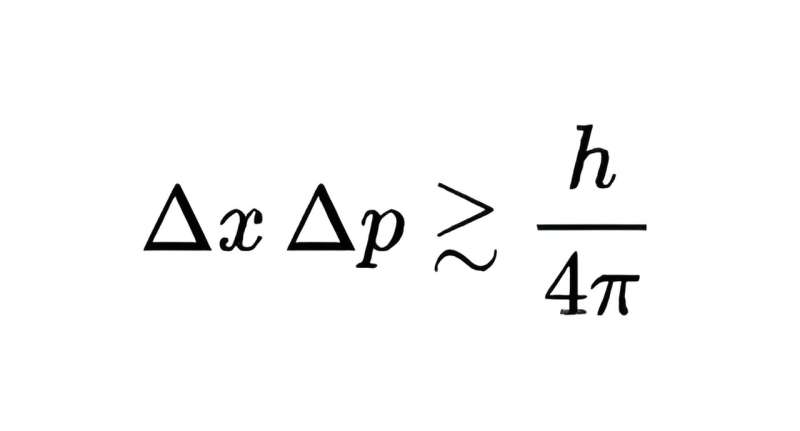
La formulation typique du principe d'incertitude. Crédit : Wikipédia, , Licence Creative Commons Attribution-Partage dans les mêmes conditions :
À proprement parler, le résultat nécessite une condition particulière qui sous-tend le théorème WAY, appelée condition de Yanase. Bien que très technique, il stipule essentiellement la compatibilité de la variable illimitée de l'appareil avec la quantité conservée. La condition de Yanase, bien que mathématique, semble recherchée par les applications aux systèmes physiques du monde réel.
“Le théorème WAY prédit qu'en vertu d'une loi de conservation, une quantité physique qui ne commute pas avec la charge conservée ne peut pas être mesurée sans erreur”, poursuit Kuramochi. “Cela correspond à une réponse à un problème ouvert vieux de 60 ans. Le nouveau résultat résout un problème vieux de plusieurs décennies sur la manière d'approcher de tels observables continus et illimités, en particulier dans des domaines comme l'optique quantique, où la nouvelle extension du théorème est susceptible de trouver des applications. “.
Le théorème WAY original interdit que l'erreur de mesure soit nulle, mais il s'agit d'un théorème qualitatif et ne précise pas la limite de mesure ni même s'il existe une limite inférieure supérieure à zéro. Il en va de même pour cette extension du théorème WAY par Kuramochi et Tajima.
Dans leur article, les auteurs écrivent que la question reste ouverte de savoir si le théorème WAY original pour les mesures répétées peut être généralisé comme ils l'ont fait, à des observables conservés illimités.
Suggérant de nouvelles directions d'investigation sur les extensions du théorème WAY, l'équipe souhaite généraliser ses résultats aux états à contrainte énergétique, car leurs résultats actuels sont limités aux cas indépendants de l'état et aux cas approximatifs. Une application potentielle consiste à fixer des limites sur la façon dont les protocoles de transmission sur réseau quantique peuvent fonctionner mieux que les limites classiques.
Plus d'information:
Yui Kuramochi et al, Théorème de Wigner-Araki-Yanase pour les observables conservés continus et illimités, Lettres d'examen physique (2023). DOI : 10.1103/PhysRevLett.131.210201
© 2023 Réseau Science X
Citation: Extension du principe d'incertitude en utilisant un opérateur illimité (2023, 14 décembre) récupéré le 14 décembre 2023 sur
Ce document est soumis au droit d'auteur. En dehors de toute utilisation équitable à des fins d'étude ou de recherche privée, aucune partie ne peut être reproduite sans autorisation écrite. Le contenu est fourni seulement pour information.
