Fusionner l’IA et les efforts humains pour résoudre des problèmes mathématiques complexes
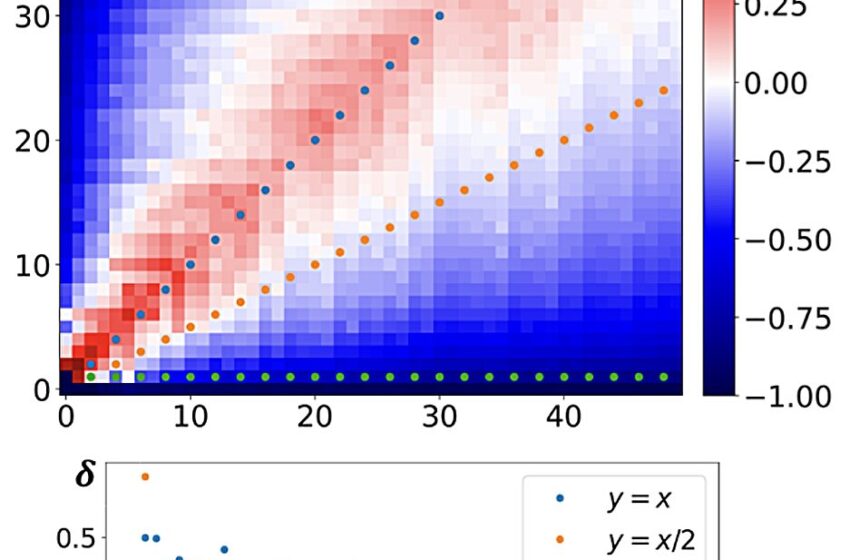
Prouver l’irrationalité en utilisant le champ matriciel conservateur. Il existe de nombreuses façons de prouver l’irrationalité d’une constante, l’une d’elles consiste à évaluer une quantité appelée « mesure d’irrationalité » (notée 𝛿). Cette mesure quantifie dans quelle mesure une séquence rationnelle peut se rapprocher d’un nombre. On peut montrer que si tous les éléments d’une séquence sont différents de la limite et que la séquence converge assez rapidement vers la limite, alors la limite est irrationnelle. Ce « assez vite » est quantifié par 𝛿, et lorsqu’il est supérieur à 0, le nombre est irrationnel. Le graphique montre la mesure d’irrationalité obtenue en chaque point du champ matriciel conservateur de la constante d’Apéry, notée ζ(3), marquant différents chemins dans le champ matriciel. Les chemins rouges fournissent des séquences avec une mesure d’irrationalité supérieure à 0, prouvant l’irrationalité de la constante ζ(3). Crédit : Elimelech et al.
En analysant rapidement de grandes quantités de données et en effectuant des prédictions précises, les outils d’intelligence artificielle (IA) pourraient aider à répondre à de nombreuses questions de recherche de longue date. Par exemple, ils pourraient aider à identifier de nouveaux matériaux pour fabriquer des produits électroniques ou les modèles d’activité cérébrale associés à des comportements humains spécifiques.
Un domaine dans lequel l’IA a jusqu’à présent été rarement appliquée est la théorie des nombres, une branche des mathématiques axée sur l’étude des nombres entiers et des fonctions arithmétiques. La plupart des questions de recherche dans ce domaine sont résolues par des mathématiciens humains, souvent des années ou des décennies après leur introduction initiale.
Des chercheurs de l’Institut israélien de technologie (Technion) ont récemment entrepris d’explorer la possibilité de résoudre des problèmes de longue date en théorie des nombres à l’aide de modèles informatiques de pointe.
Dans un article récent, publié dans le Actes de l’Académie nationale des sciencesils ont démontré qu’une telle approche informatique peut soutenir le travail des mathématiciens, les aidant à faire de nouvelles découvertes passionnantes.
“Les algorithmes informatiques dominent de plus en plus dans la recherche scientifique, une pratique désormais largement appelée” IA pour la science “”, ont déclaré Rotem Elimelech et Ido Kaminer, auteurs de l’article, à Phys.org.
“Cependant, dans des domaines comme la théorie des nombres, les progrès sont souvent attribués à la créativité ou à l’intuition humaine. Dans ces domaines, des questions peuvent rester sans réponse pendant des centaines d’années, et même si trouver une réponse peut être aussi simple que de découvrir la formule correcte, il n’y a pas de solution.” une voie claire pour y parvenir.
Elimelech, Kaminer et leurs collègues ont exploré la possibilité que les algorithmes informatiques puissent automatiser ou augmenter l’intuition mathématique. Cela les a inspirés à créer le groupe de recherche Ramanujan Machine, un nouvel effort de collaboration visant à développer des algorithmes pour accélérer la recherche mathématique.
Leur groupe de recherche pour cette étude comprenait également Ofir David, Carlos de la Cruz Mengual, Rotem Kalisch, Wolfram Berndt, Michael Shalyt, Mark Silberstein et Yaron Hadad.
“Sur le plan philosophique, notre travail explore l’interaction entre les algorithmes et les mathématiciens”, expliquent Elimelech et Kaminer. “Notre nouvel article montre en effet que les algorithmes peuvent fournir les données nécessaires pour inspirer des idées créatives, conduisant à la découverte de nouvelles formules et de nouvelles connexions entre constantes mathématiques.”

Crédit : Elimelech et al.
Le premier objectif de l’étude récente d’Elimélec, Kaminer et de leurs collègues était de faire de nouvelles découvertes sur les constantes mathématiques. Tout en travaillant vers cet objectif, ils ont également entrepris de tester et de promouvoir des approches alternatives pour mener des recherches en mathématiques pures.
“Le ‘champ matriciel conservateur’ est une structure analogue au champ vectoriel conservateur que chaque étudiant en mathématiques ou en physique apprend en première année de premier cycle”, ont expliqué Elimelech et Kaminer. “Dans un champ vectoriel conservateur, tel que le champ électrique créé par une particule chargée, nous pouvons calculer le changement de potentiel à l’aide d’intégrales de ligne.
“De même, dans les champs matriciels conservateurs, nous définissons un potentiel sur un espace discret et le calculons par des multiplications matricielles plutôt que par des intégrales linéaires. Voyager entre deux points équivaut à calculer la variation du potentiel et implique une série de multiplications matricielles. “
Contrairement au champ vectoriel conservateur, le champ matriciel conservateur est une nouvelle découverte. Un avantage important de cette structure est qu’elle peut généraliser les formules de chaque constante mathématique, générant ainsi une infinité de nouvelles formules du même type.
“La façon dont le champ matriciel conservateur crée une formule consiste à voyager entre deux points (ou en fait, à voyager d’un point jusqu’à l’infini à l’intérieur de son espace discret)”, ont déclaré Elimelech et Kaminer. “Trouver des champs matriciels non triviaux qui sont également conservateurs est un défi.”
Dans le cadre de leur étude, Elimelech, Kaminer et leurs collègues ont utilisé l’informatique distribuée à grande échelle, ce qui implique l’utilisation de plusieurs nœuds interconnectés travaillant ensemble pour résoudre des problèmes complexes. Cette approche leur a permis de découvrir de nouvelles séquences rationnelles qui convergent vers des constantes fondamentales (c’est-à-dire des formules pour ces constantes).
“Chaque séquence représente un chemin caché dans le champ matriciel conservateur”, ont expliqué Elimelech et Kaminer. “À partir de la variété de ces chemins, nous avons procédé à une ingénierie inverse du champ matriciel conservateur. Nos algorithmes ont été distribués à l’aide de BOINC, une infrastructure de calcul volontaire. Nous sommes reconnaissants de la contribution de centaines d’utilisateurs dans le monde qui ont fait don de leur temps de calcul au cours des deux dernières années et un an et demi, rendant cette découverte possible.”
Les travaux récents de l’équipe de recherche du Technion démontrent que les mathématiciens peuvent bénéficier plus largement de l’utilisation d’outils et d’algorithmes informatiques pour leur fournir un « laboratoire virtuel ». De tels laboratoires offrent l’occasion de tester des idées expérimentalement sur un ordinateur, ressemblant aux expériences réelles disponibles en physique et dans d’autres domaines scientifiques. Plus précisément, les algorithmes peuvent réaliser des expériences mathématiques en fournissant des formules pouvant être utilisées pour formuler de nouvelles hypothèses mathématiques.
“Ces hypothèses, ou conjectures, font avancer la recherche mathématique”, ont déclaré Elimelech et Kaminer. “Plus il y a d’exemples soutenant une hypothèse, plus elle devient forte, augmentant ainsi la probabilité qu’elle soit correcte. Les algorithmes peuvent également découvrir des anomalies, pointant vers des phénomènes qui sont les éléments constitutifs de nouvelles hypothèses. De telles découvertes ne seraient pas possibles sans une approche mathématique à grande échelle. expériences qui utilisent l’informatique distribuée.
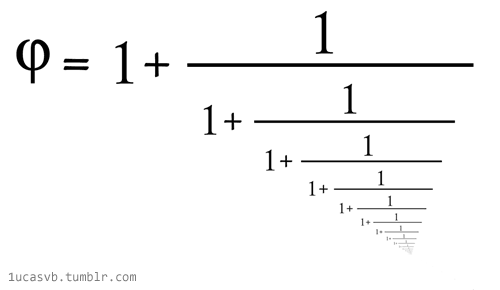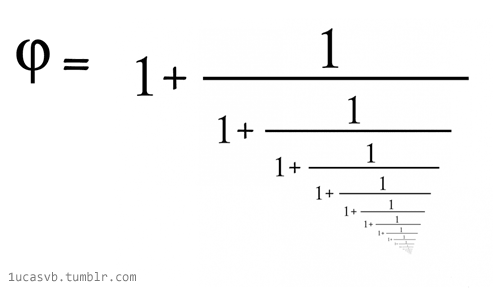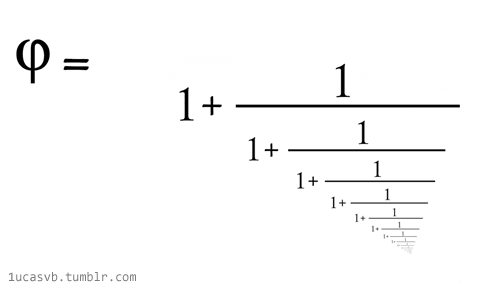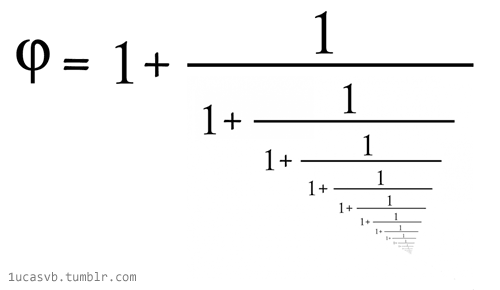
Crédit: Actes de l’Académie nationale des sciences (2024). DOI : 10.1073/pnas.2321440121
Un autre aspect intéressant de cette étude récente est qu’elle démontre les avantages de la création de communautés pour résoudre les problèmes. En fait, les chercheurs ont publié leur code en ligne dès les premiers jours de leur projet et se sont appuyés sur les contributions d’un vaste réseau de bénévoles.
“Notre étude montre que la recherche scientifique peut être menée sans accès exclusif aux superordinateurs, ce qui représente un pas substantiel vers la démocratisation de la recherche scientifique”, ont déclaré Elimelech et Kaminer. “Nous publions régulièrement des hypothèses non prouvées générées par nos algorithmes, mettant au défi d’autres passionnés de mathématiques d’essayer de prouver ces hypothèses, qui, une fois validées, sont publiées sur le site Web de notre projet. Cela s’est produit à plusieurs reprises jusqu’à présent. L’un des contributeurs de la communauté, Wolfgang Berndt, l’a compris. impliqué qu’il fait désormais partie de notre équipe principale et qu’il est co-auteur de l’article.
La nature collaborative et ouverte de cette étude a permis à Elimelech, Kaminer et au reste de l’équipe d’établir de nouvelles collaborations avec d’autres mathématiciens du monde entier. En outre, leurs travaux ont suscité l’intérêt de certains enfants et jeunes, leur montrant comment les algorithmes et les mathématiques peuvent être combinés de manière fascinante.
Dans leurs prochaines études, les chercheurs prévoient de développer davantage la théorie des champs matriciels conservateurs. Ces champs matriciels constituent un outil très puissant pour générer des preuves d’irrationalité pour des constantes fondamentales, avec lesquels Elimelech, Kaminer et l’équipe prévoient de continuer à expérimenter.
“Notre objectif actuel est d’aborder les questions concernant l’irrationalité de constantes célèbres dont l’irrationalité est inconnue, restant parfois une question ouverte pendant plus de cent ans, comme dans le cas de la constante catalane”, ont déclaré Elimelech et Kaminer.
“Un autre exemple est la fonction zêta de Riemann, centrale dans la théorie des nombres, avec ses zéros au cœur de l’hypothèse de Riemann, qui est peut-être le problème non résolu le plus important en mathématiques pures. De nombreuses questions restent ouvertes sur les valeurs de cette fonction, notamment l’irrationalité de ses valeurs. Plus précisément, la question de savoir si ζ(5) est irrationnelle est une question ouverte qui attire les efforts des grands mathématiciens.
Le but ultime de cette équipe de chercheurs est d’utiliser avec succès leur approche mathématique expérimentale pour prouver l’irrationalité d’une de ces constantes. À l’avenir, ils espèrent également appliquer systématiquement leur approche à un éventail plus large de problèmes de mathématiques et de physique. Leur style de recherche pratique inspiré de la physique découle de la nature interdisciplinaire de l’équipe, qui regroupe des personnes spécialisées en CS, EE, mathématiques et physique.
“Notre groupe Ramanujan Machine peut aider d’autres chercheurs à créer des algorithmes de recherche pour leurs problèmes importants, puis à utiliser l’informatique distribuée pour effectuer des recherches sur de grands espaces, ce qui ne pourrait être tenté autrement”, ont ajouté Elimelech et Kaminer. “Chacun de ces algorithmes, s’il réussit, contribuera à mettre en évidence de nouveaux phénomènes et éventuellement de nouvelles hypothèses en mathématiques, aidant ainsi à choisir des directions de recherche prometteuses. Nous envisageons maintenant de faire avancer cette stratégie en mettant en place un espace utilisateur virtuel pour les mathématiques expérimentales”, inspiré par la longue histoire et l’impact des installations utilisateur pour la physique expérimentale.
Plus d’information:
Rotem Elimelech et al, Découverte assistée par algorithme d’un ordre intrinsèque parmi les constantes mathématiques, Actes de l’Académie nationale des sciences (2024). DOI : 10.1073/pnas.2321440121
© 2024 Réseau Science X
Citation: Fusionner l’IA et les efforts humains pour résoudre des problèmes mathématiques complexes (24 juin 2024) récupéré le 24 juin 2024 sur
Ce document est soumis au droit d’auteur. En dehors de toute utilisation équitable à des fins d’étude ou de recherche privée, aucune partie ne peut être reproduite sans autorisation écrite. Le contenu est fourni seulement pour information.
